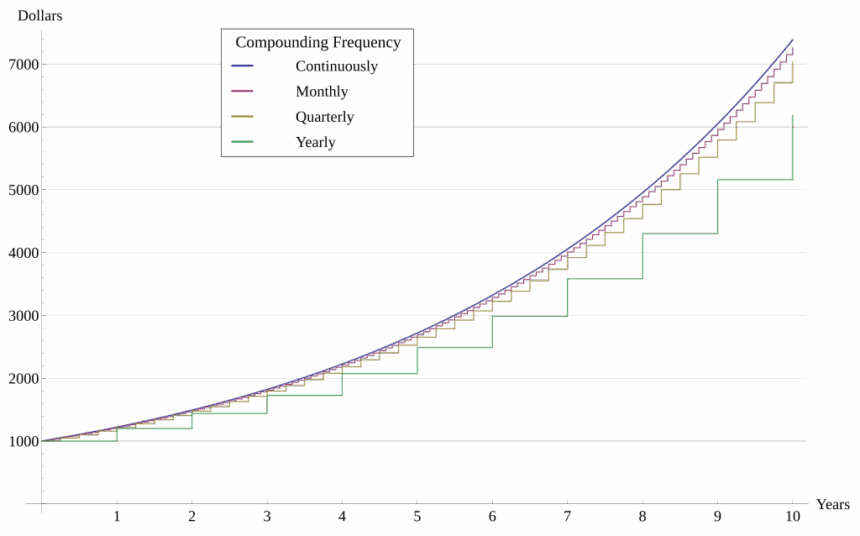
In this article, I will discuss what is the formula for compound interest and explain how it works in simple terms. Compound interest helps your money grow faster by earning interest on both the principal and the accumulated interest.
Understanding the formula behind it can help you make smarter financial decisions, whether you’re saving, investing, or borrowing.
About Compound Interest
According to its definition, compound interest is the interest calculated on both initial principal and accumulated interest from previous terms. This gives money the ability to grow exponentially instead of linearly, which is important when it comes to investing or saving money for the long-term.
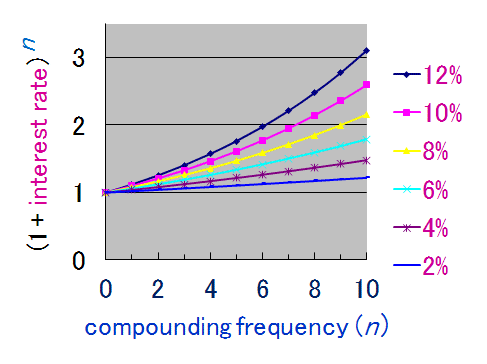
Let’s see an example. When you invest $1,000 at an interest rate of 5% which is compounded yearly, by the end of the year you will have $1,050. For the second year, the interest will be calculated on $1,050 instead of the original $1,000, allowing for even higher returns over time.
The Compound Interest Formula
The general formula for calculating compound interest is: A=P(1+rn)ntA = P \left(1 + \frac{r}{n}\right)^{nt}A=P(1+nr)nt
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment or loan amount (initial amount)
- r = the annual nominal interest rate (as a decimal)
- n = the number of times the interest is compounded per year
- t = the number of years the money is invested or borrowed
Breaking Down the Components
Let’s take a look at each part of the formula in order to understand how compound interest functions:
Principal (P): This is your starting amount. When you’re saving or borrowing, your initial amount affects the situation greatly over a long period of time.
Interest Rate (r): Given as a decimal (5% would be 0.05), it is the rate at which your currency increases.

Compounding Frequency (n): How often interest gets added to the principal is described here. Common frequencies are once a year (n=1), two times a year (n=2), every three months (n=4), every month (n=12), or every day (n=365).
Time (t): The number of years you allow your money to grow (or the duration of the loan).
Example: Calculating Compound Interest
Let’s walk through a simple example.
Scenario: You invest $5,000 in a savings account with an annual interest rate of 6%, compounded monthly, for 3 years.
Using the formula:
- P = $5,000
- r = 0.06
- n = 12 (monthly compounding)
- t = 3
A=5000(1+0.0612)12×3=5000(1+0.005)36=5000(1.005)36=5000×1.1967=5983.50A = 5000 \left(1 + \frac{0.06}{12}\right)^{12 \times 3} = 5000 \left(1 + 0.005\right)^{36} = 5000 \left(1.005\right)^{36} = 5000 \times 1.1967 = 5983.50A=5000(1+120.06)12×3=5000(1+0.005)36=5000(1.005)36=5000×1.1967=5983.50
So, after 3 years, your investment would grow to approximately $5,983.50, earning $983.50 in interest.
The Power of Compounding Over Time
Over extended periods of time, compound interest yields the greatest results. Starting from the initial stages of investing or saving is heavily emphasized by financial advisors. Differences in interest rates and the frequency of compounding greatly affect the final yield.
Comparison Example:
- Invest $10,000 at 5% for 10 years, compounded annually:
A=10,000(1+0.05)10=10,000×1.6289=16,289A = 10,000 (1 + 0.05)^10 = 10,000 \times 1.6289 = 16,289A=10,000(1+0.05)10=10,000×1.6289=16,289
- Invest the same amount for 30 years:
A=10,000(1+0.05)30=10,000×4.3219=43,219A = 10,000 (1 + 0.05)^30 = 10,000 \times 4.3219 = 43,219A=10,000(1+0.05)30=10,000×4.3219=43,219
Over 30 years, the investment more than quadruples, showing the exponential nature of compound interest.
Continuous Compounding
In some cases, interest is compounded continuously, meaning it is added at every possible instant. The formula for continuous compounding is: A=PertA = Pe^{rt}A=Pert
Where e is Euler’s number (approximately 2.71828).
For instance, if you invest $1,000 at 7% interest for 5 years, continuously compounded: A=1000×e0.07×5=1000×e0.35=1000×1.419=1419A = 1000 \times e^{0.07 \times 5} = 1000 \times e^{0.35} = 1000 \times 1.419 = 1419A=1000×e0.07×5=1000×e0.35=1000×1.419=1419
Real-World Applications
Compound interest applies in different areas of finance: In savings accounts or certicates of deposit (CDs) As part of retirement plans like a 401k or IRA With credit cards (interest on outstanding payments) Mortgages and other long-term loans Projections concerning the growth of investments
Knowing how these systems work allows a person to make smarter decisions when it comes to finances, their maximized return, and their minimized debt.
Conclusion
Although the compound interest formula might seem complicated at first glance, it is useful for anyone wanting to increase their assets or streamline debt. Knowing the factors of the formula will assist in making a better decision regarding saving, spending, investing, or taking loans.
If you start utilizing compound interest early on, its effects will benefit you more. Your best friend when it comes to finances turns out to be time.