In this post, I will explain What Is The Formula For The Volume Of A Cone. It is crucial to grasp this calculation when determining the space within cone-shaped items.
Whether it’s during class or in the real world, the ability to compute the volume of a cone aids in resolving numerous issues concerning geometrical figures like ice cream cones, funnels, or per architectural structures.
Understanding the Formula for the Volume of a Cone
Geometry, as one of the wonders of mathematics, concerns itself with the properties of a space and its sizes, shapes and volumes. There are numerous types of three-dimensional shapes and we frequently come across a cone in our day to day life.
The plethora of shapes which exist in life includes ice-cream cones and traffic cones. It is sometimes baffling to learn how to calculate the volume of cones. Ice cream cones and traffic cones are common examples, but understanding how to calculate their volume is often puzzling.
In this article, we will examine the mathematical formula cone volume calculations, where we derive its formula and find ways to apply it in the real world, solving one of the fundamental problems in geometry.
What is a Cone?
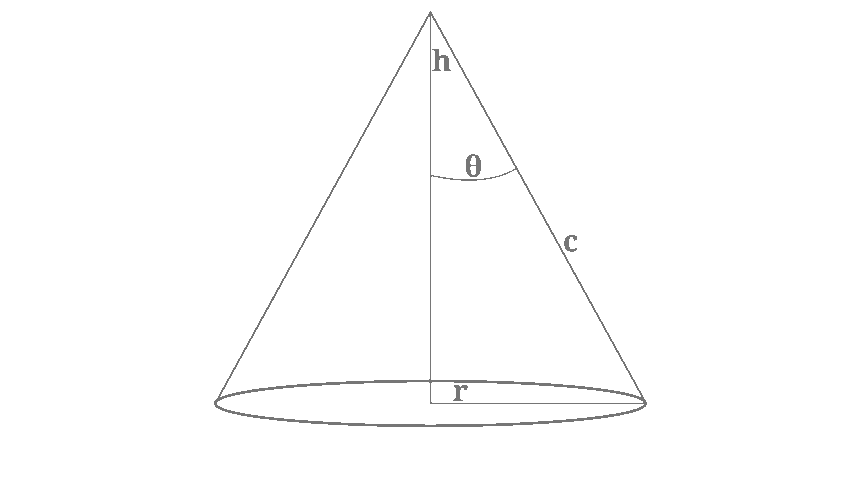
A cone can be described as a three-dimensional geometrical shape which tapers from a flat, circular base to a point which is called apex or vertex.

The base is a circle, and the apex is connected to the base of the cone by a straight line which sweeps to from the surface of the cone.
Cones are divided into two types:
Right Circular Cone: When the apex is directly above the center of the circular base, which makes the cone’s axis perpendicular to the base.
Oblique Cone: When the apex is not positioned directly above the center of the base.
The focus of this article will be the right circular cone, as it is the most studied cone being the easiest to calculate in terms of volume.
The Formula for the Volume of a Cone
The volume VVV of a cone is the amount of space enclosed within its surfaces. The standard formula for the volume of a right circular cone is: V=13πr2hV = \frac{1}{3} \pi r^2 hV=31πr2h
Where:
- VVV = volume of the cone,
- rrr = radius of the circular base,
- hhh = height of the cone (the perpendicular distance from the base to the apex),
- π\piπ (pi) ≈ 3.14159, a mathematical constant representing the ratio of the circumference of a circle to its diameter.
Breaking Down the Formula
- πr2\pi r^2πr2: This part represents the area of the circular base of the cone. Since the base is a circle, its area is calculated with the formula for the area of a circle, which is πr2\pi r^2πr2.
- hhh: This is the height of the cone, a measure of how tall it stands from the base to the tip.
- 13\frac{1}{3}31: The volume of a cone is exactly one-third of the volume of a cylinder with the same base and height. This factor 13\frac{1}{3}31 adjusts for the tapering shape of the cone.
Why One-Third?
You might ask yourself why a cone’s volume is exactly one-third that of a cylinder that shares its base and height. This relation is basic in geometry, and it can be proved either through calculus or by geometric techniques.
Imagine a cylinder and a cone placed side by side, both with radius rrr and height hhh. The cylinder’s volume is:
Vcylinder=πr2h
If you could fill the cone with water and pour it into the cylinder, you would find it takes exactly three full cones to fill the cylinder. Hence, the volume of the cone is one-third of the cylinder’s volume.
Practical Applications of the Volume Formula
Real-world examples that cones come in handy are:
Engineering: Determining the volume of conical objects depictions like funnels, nozzles, or tanks.
Food Industry: Determining the volume of delicious treats such as ice cream or cake shaped in cones.
Architecture: Estimating the structural value of roofs or spires with conical shapes.
Environmental Science: Estimating the volume of the curious cones a volcano may form in order to determine the scales of an eruption.
Real Life: Estimating the volume in which a party hat or funnel-shaped traffic cone may occupy.
Conclusion
To sum up, the volume of a cone is given in the formula $V = \frac{1}{3} \pi r^2 h$, where radius is denoted by $r$ and height by $h$.
This means that the volume of the cone is one third of the cylinder which has the same base and height, assisting in computing the space within conical shapes in various practical and mathematical applications.