How To Solve Logarithmic Equations: Simple Step-by-Step Guide

In this guide, I will explain how to solve logarithmic equations step by step. I will teach you to isolate the logs, apply important properties, change equations to exponential form, and check all solutions.

These strategies will work whether you are solving math homework or applying mathematics in science or finance, helping you work through logarithmic issues easily and effectively.

Brief Explanation Logarithmic Equations

An equation whose variable appears in logarithm form is called a logarithmic equation. It usually takes the shape “log_bx = c” which translates to “the power you raise b to get x equals c.

Solving logarithmic equations often requires rewriting them in exponential format, utilizing certain principles such as product, quotient, or power rules to condense or simplify the logs.

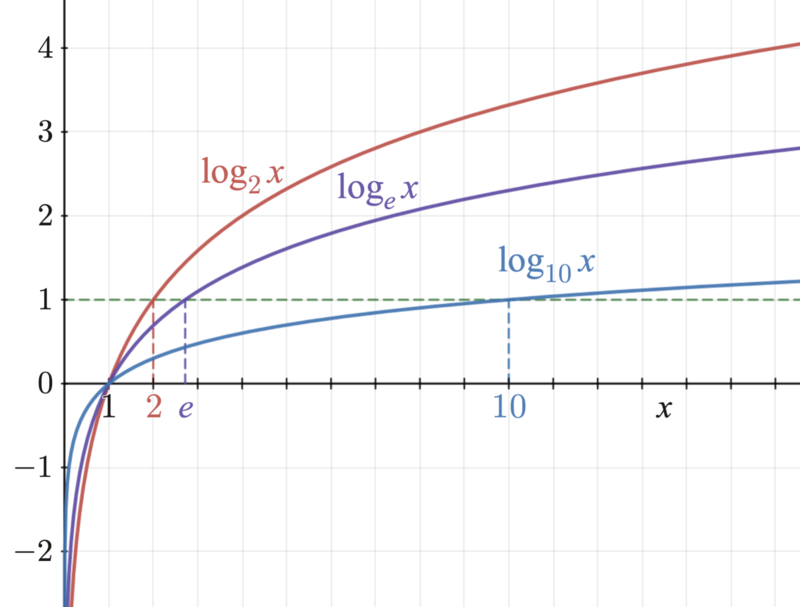
Since logarithms are defined only for positive value real numbers, it is essential to check each step towards the solution to verify its validity.

Such these equations are commonplace in many fields including science, engineering, and finance to describe growth, decay, and complex scaling.

How To Solve Logarithmic Equations

Sure! Here’s a short example using a single platform (logarithm base) to show how to solve a logarithmic equation step by step:

Example: Solve log₂(x – 3) = 4

Step 1: Recognize the form

This is a logarithmic equation with a single logarithm: log⁡2(x−3)=4\log_2(x – 3) = 4

Step 2: Rewrite in exponential form

Use the definition: log⁡b(a)=c⟺bc=a\log_b(a) = c \quad \Longleftrightarrow \quad b^c = a

So: 24=x−32^4 = x – 3 16=x−316 = x – 3

Step 3: Solve for x

x=16+3x = 16 + 3 x=19x = 19

Step 4: Check the solution

Ensure the argument of the log is positive: x−3=19−3=16>0x – 3 = 19 – 3 = 16 > 0

Why Solving Logarithmic Equations is Important

Logarithmic equations are important in solving unknowns in problems involving exponential growth & decay such as, in population modeling and financia, compound interest, and in radioactive half-life.

In engineering and science logarithmic functions help manage extremely minute or immense values, for instances decibels or pH levels.

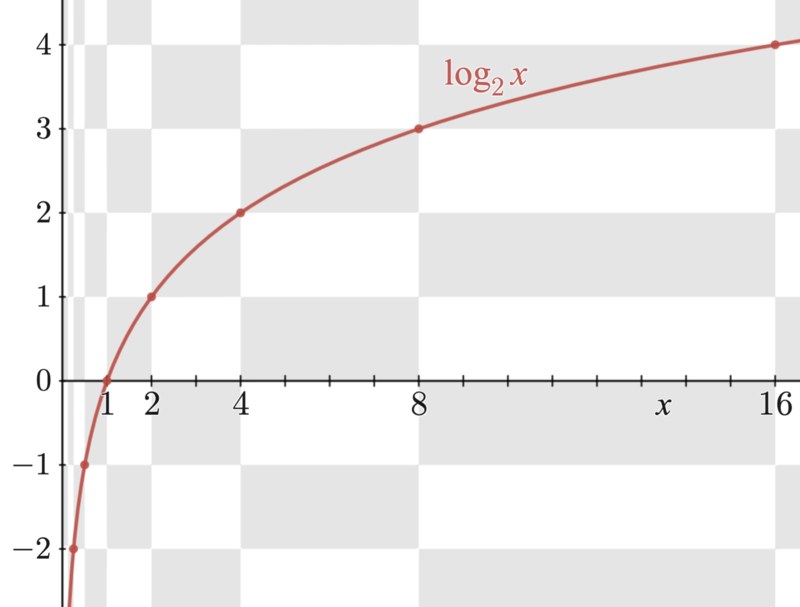
In computer science logarithm defines the magnitude of the algorithm’s complexity (log(n)). Logarithmic equations equip us to master interpret data and accurate pattern forecasting enabling better decisions resolving substantial matters in technology, economy, natural science spheres.

Types of Logarithmic Equations

Single logarithm equations:Formed as a singular logarithm equal to a constant or number and solved by rewriting in exponential form.

Equations with logs on both sides:Logarithmic expressions appear on both sides of the equation, enabling comparison of arguments when bases are the same.

Equations requiring logarithm properties to combine:Contain many logs on one side which necessitates the application of product, quotient, or power rules to combine.

Common Pitfalls and How to Avoid Them

Neglect Check for Domain Restrictions

Always check back-substituted solutions for invalid or extraneous values outside the domain to keep logarithm arguments positive.

Verification is No Solution Return

Use the original equation to verify every result. Ensure the result satisfies the original to avoid extraneous or inadmissible solutions.

Ignoring Rules for Logarithms

Application of product, quotient, and power rules should always be done with caution; errors here distort equations and create wrong solutions.

Practice Problems

List of 4–6 problems of varying difficulty for the reader to try:Include straightforward along with advanced logarithmic expressions where readers isolate logs, combine them, and verify domains to construct robust problem-solving skills.

Optionally include brief answers:Provide concise responses or final values so readers validate their calculations independently, strengthening concepts and enhancing confidence through instant feedback on their efforts.

Conclusion

To finalize, making the most out of solving logarithmic equations requires definition of bounds, straightforward isolating of the logarithm, rewriting in exponential form, as well as solving step by step.

Logarithmic equations require their solutions checked, and to ensure that the arguments are always positive.

After repeated practice, a logarithmic equation solves with ease for real life problems such as growth or decay in mathematics and science as well as finance, and technology.

FAQ